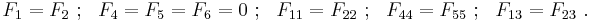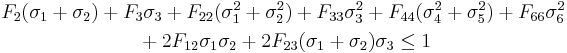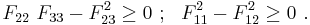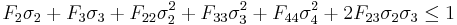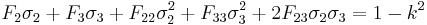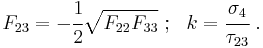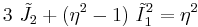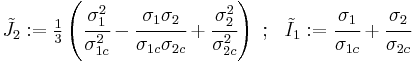Tsai–Wu failure criterion
The Tsai–Wu failure criterion[1] is a phenomenological failure theory which is widely used for anisotropic composite materials which have different strengths in tension and compression. This failure criterion is a specialization of the general quadratic failure criterion proposed by Gol'denblat and Kopnov[2] and can be expressed in the form
where 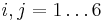 and repeated indices indicate summation, and
and repeated indices indicate summation, and 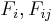 are experimentally determined material strength parameters. The stresses
are experimentally determined material strength parameters. The stresses 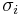 are expressed in Voigt notation. If the failure surface is to be closed and convex, the interaction terms
are expressed in Voigt notation. If the failure surface is to be closed and convex, the interaction terms 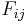 must satisfy
must satisfy
which implies that all the 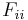 terms must be positive.
terms must be positive.
Contents |
Tsai–Wu failure criterion for orthotropic materials
For orthotropic materials with three planes of symmetry oriented with the coordinate directions, if we assume that 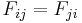 and that there is no coupling between the normal and shear stress terms (and between the shear terms), the general form of the Tsai–Wu failure criterion reduces to
and that there is no coupling between the normal and shear stress terms (and between the shear terms), the general form of the Tsai–Wu failure criterion reduces to
Let the failure strength in uniaxial tension and compression in the three directions of anisotropy be 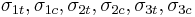 . Also, let us assume that the shear strengths in the three planes of symmetry are
. Also, let us assume that the shear strengths in the three planes of symmetry are 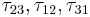 (and have the same magnitude on a plane even if the signs are different). Then the coefficients of the orthotropic Tsai–Wu failure criterion are
(and have the same magnitude on a plane even if the signs are different). Then the coefficients of the orthotropic Tsai–Wu failure criterion are
The coefficients 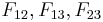 can be determined using equibiaxial tests. If the failure strengths in equibiaxial tension are
can be determined using equibiaxial tests. If the failure strengths in equibiaxial tension are 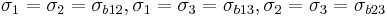 then
then
The near impossibility of performing these equibiaxial tests has led to there being a severe lack of experimental data on the parameters 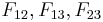 .
.
It can be shown that the Tsai-Wu criterion is a particular case of the generalized Hill yield criterion [3].
Tsai-Wu failure criterion for transversely isotropic materials
For a transversely isotropic material, if the plane of isotropy is 1–2, then
Then the Tsai-Wu failure criterion reduces to
where 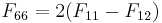 . This theory is applicable to a unidirectional composite lamina where the fiber direction is in the '3'-direction.
. This theory is applicable to a unidirectional composite lamina where the fiber direction is in the '3'-direction.
In order to maintain closed and ellipsoidal failure surfaces for all stress states, Tsai and Wu also proposed stability conditions which take the following form for transversely isotropic materials
Tsai–Wu failure criterion in plane stress
For the case of plane stress with 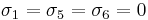 , the Tsai–Wu failure failure criterion reduces to
, the Tsai–Wu failure failure criterion reduces to
The strengths in the expressions for 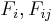 may be interpreted, in the case of a lamina, as
may be interpreted, in the case of a lamina, as 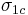 = transverse compressive strength,
= transverse compressive strength, 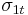 = transverse tensile strength,
= transverse tensile strength, 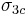 = longitudinal compressive strength,
= longitudinal compressive strength, 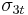 = longitudinal strength,
= longitudinal strength, 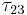 = longitudinal shear strength,
= longitudinal shear strength, 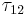 = transverse shear strength.
= transverse shear strength.
Tsai–Wu criterion for foams
The Tsai–Wu criterion for closed cell PVC foams under plane strain conditions may be expressed as
where
For Divinyl H250 PVC foam (density 250 kg/cu.m.), the values of the strengths are 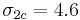 MPa,
MPa, 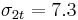 MPa,
MPa, 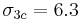 MPa,
MPa, 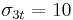 MPa [4].
MPa [4].
For aluminum foams in plane stress, a simplified form of the Tsai–Wu criterion may be used if we assume that the tensile and compressive failure strengths are the same and that there are no shear effects on the failure strength. This criterion may be written as [5]
where
Tsai–Wu criterion for bone
The Tsai–Wu failure criterion has also been applied to trabecular bone/cancellous bone[6] with varying degrees of success. The quantity 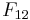 has been shown to have a nonlinear dependence on the density of the bone.
has been shown to have a nonlinear dependence on the density of the bone.
References
- ^ Tsai, S. W. and Wu, E. M. (1971). A general theory of strength for anisotropic materials. Journal of Composite Materials. vol. 5, pp. 58–80.
- ^ Gol'denblat, I. and Kopnov, V. A. (1966). Strength of glass reinforced plastic in the complex stress state. Polymer Mechanics, vol. 1, pp. 54–60. (Russian: Mechanika Polimerov, vol. 1, pp. 70–78. 1965)
- ^ Abrate, S. (2008). Criteria for yielding or failure of cellular materials Journal of Sandwich Structures and Materials, vol. 10, pp. 5–51.
- ^ Gdoutos, E. E., Daniel, I. M. and Wang, K-A. (2001). Multiaxial characterization and modeling of a PVC cellular foam. Journal of Thermoplastic Composite Materials, vol. 14, pp. 365–373.
- ^ Duyoyo, M. and Wierzbicki, T. (2003). Experimental studies on the yield behavior of ductile and brittle aluminum foams. International Journal of Plasticity, vol. 19, no. 8, pp. 1195–1214.
- ^ Keaveny, T. M., Wachtel, E. F., Zadesky, S. P., Arramon, Y. P. (1999). Application of the Tsai–Wu quadratic multiaxial failure criterion to bovine trabecular bone. ASME Journal of Biomechanical Engineering, vol. 121, no. 1, pp. 99–107.
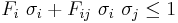
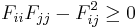
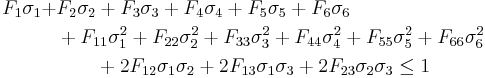
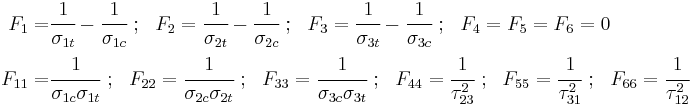
![\begin{align}
F_{12} &= \cfrac{1}{2\sigma_{b12}^2}\left[1-\sigma_{b12}(F_1%2BF_2)-\sigma_{b12}^2(F_{11}%2BF_{22})\right]\\
F_{13} &= \cfrac{1}{2\sigma_{b13}^2}\left[1-\sigma_{b13}(F_1%2BF_3)-\sigma_{b13}^2(F_{11}%2BF_{33})\right] \\
F_{23} &= \cfrac{1}{2\sigma_{b23}^2}\left[1-\sigma_{b23}(F_2%2BF_3)-\sigma_{b23}^2(F_{22}%2BF_{33})\right]
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/53aba4242c621d6d768c9a921d9e5fac.png)